Énigme
cEoudccssEé + dunrEnnssuo
Le résultat de cette somme est la solution à tous vos problèmes de mathématiques décisionnelles ! 😉
Quelle est la valeur de chacune des lettres ?
Méthode de résolution
Le résultat de la somme cEoudccssEé + dunrEnnssuo est bien sûr Eurodécision !
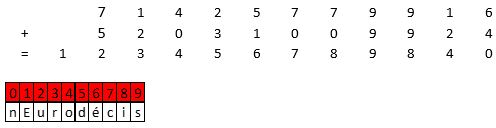
Posons cette addition :

La somme de 2 chiffres différents est <=18 + la retenue éventuelle de 2 nombres à 11 chiffres qui donne un nombre à 12 chiffres : E =1. Remplaçons cette valeur dans l’addition.

Les valeurs des lettres étant toutes différentes, nous allons suivre les affectations réalisées et les possibilités restantes (en rouge les valeurs déjà affectées) :
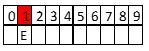
Colonne jaune : c+n=c => (n=0 si pas de retenue) ou (c+n+1=10+c si retenue) => (n=0) ou (n=9). Mais si n=9, on a : (colonne jaune c+n+1=c+10) et (colonne verte c+n=i >10 car il y a une retenue, et colonne rose (2s=s) => s=0 ; or colonne bleue (2s=i si pas de retenue) ou (2s+1=i si retenue) => comme s=0, i=1 mais on a déjà E=1. Donc n≠9, donc n=0.
Mise à jour de l’addition et des affectations :

Colonne rose : s≠0 (valeur déjà affectée) donc il y a une retenue : 2s+1=10+s => s=9
Mise à jour de l’addition et des affectations :

Colonne rose : 9+9+1=19 (il y a forcément une retenue) ; colonne bleue : (9+9+1=i+10 si retenue) ou (9+9=10+i si pas de retenue). 9+9+1=i+10 implique i=9, ce qui n’est pas possible (valeur déjà affectée), on a donc (9+9=10+i), soit i=8.
Mise à jour de l’addition et des affectations :

Colonne verte : (c+0+1=8 si retenue) ou (c+0=8 si pas de retenue), soit c=7 ou c=8. Comme la valeur 8 est déjà affectée, c=7.
Mise à jour de l’addition et des affectations :

Colonne jaune : é+o=10 => (é=4 et o=6) ou (é=6 et o=4). Colonne verte : 1+1+u=o. Donc si o=4 on a u=2 et é=6 ; si o=6 on a u=4=é, ce qui n’est pas possible. Donc u=2, o=4, é=6.
Mise à jour de l’addition et des affectations :
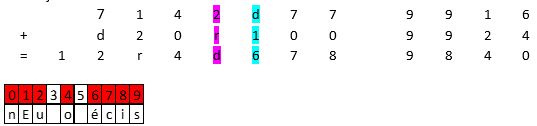
Colonne bleue : d+1=6 => d=5. Colonne rose : 2+r=d soit 2+r=5, donc r=3.
Mise à jour de l’addition et des affectations donnant la solution finale :