Que ce soit dans le domaine de la santé, de l’industrie, en marketing, en finance ou dans d’autres secteurs, les applications du Machine Learning sont partout. Toutefois, afin de mener à bien ces projets, de bonnes analyses et interprétations statistiques sont indispensables pour extraire des connaissances utiles à partir des données brutes. Dans cet article, nous présenterons des exemples de pièges statistiques qui peuvent compromettre différentes étapes d’un projet d’analyse de données et mener à de faux résultats.
Corrélation n’est pas causalité
La corrélation est une statistique qui permet de montrer l’existence ou l’absence d’une relation entre deux variables sur un même groupe d’observations. Ainsi, nous pouvons dire par exemple que l’âge et la taille d’une personne sont corrélés positivement. Cependant, même si cela peut être tentant dans cet exemple, nous ne pouvons en aucun cas en déduire un lien de cause à effet entre les deux phénomènes. En statistiques, cela est rappelé par la locution latine « cum hoc sed non propter » qui veut dire « avec ceci, cependant pas à cause de ceci ».
Pourtant, cette erreur d’interprétation est très répandue et peut avoir des conséquences importantes dans la compréhension des données et la modélisation d’un problème.
Dans son livre « Spurious correlation », Tyler Vigen montre de manière drôle mais efficace à quel point cette erreur de compréhension de la notion de corrélation peut amener à des conclusions absurdes. Nous apprenons par exemple qu’il y a une corrélation entre le taux de divorce dans le Maine et la consommation de Margarine ainsi qu’entre le nombre de films dans lesquels Nicolas Cage a joué et le nombre de décès en se noyant dans une piscine. Si nous soutenons qu’une corrélation implique une causalité, il serait urgent de bannir la margarine de nos recettes et de mettre fin à la carrière de l’acteur américain.
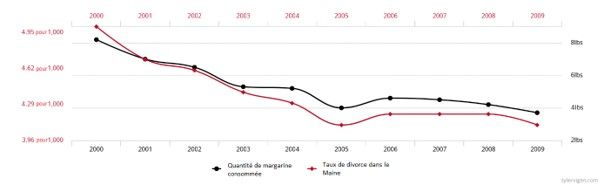
Corrélation entre le taux de divorce dans le Maine et la consommation de Margarine par habitant
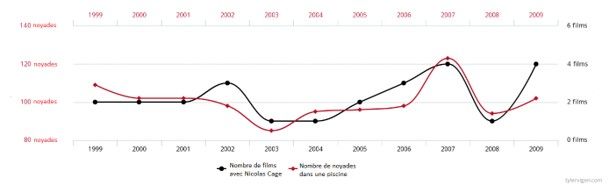
Corrélation entre le nombre de décès par noyade dans une piscine et le nombre de films de Nicolas Cage
Moyenne ou médiane ?
La médiane est une des notions statistiques les plus simples et les plus utiles mais dont l’utilisation n’est malheureusement pas aussi fréquente que la moyenne. Pourtant, dans plusieurs situations, l’utilisation de la médiane peut s’avérer plus pertinente pour synthétiser des données.
Si nous prenons l’exemple d’un groupe de cinq personnes qui gagnent respectivement 2000, 2500, 2200, 2300 et 100 000 euros par mois, nous dirons qu’une personne dans ce groupe gagne en moyenne 21 800 euros mensuellement. Cela peut sembler « faux », mais c’est bien une moyenne que nous avons calculée. Sur le même échantillon, en calculant la médiane, nous obtenons 2300 euros.
Dans cet exemple, le grand écart entre la médiane et la moyenne est dû à la présence du salaire mensuel 100 000 euros, que nous appelons en statistiques un point aberrant. L’avantage donc de la médiane est qu’elle ne prend pas en compte ces points dans son calcul, contrairement à la moyenne.
Ainsi, dans le cas des salaires des habitants d’un pays, le salaire moyen donne une idée de ce que chaque habitant gagnerait si tous les habitants avaient le même salaire et le salaire médian nous indique qu’il y a 50% d’habitants qui gagnent plus et 50% d’habitants qui gagnent moins que cette valeur.
Il en va de même dans tous les projets d’analyse de données où il est important de savoir choisir entre la médiane et la moyenne pour estimer la tendance centrale d’un groupe d’observations.
Le paradoxe de Simpson
Le choix du groupe ou de la maille à laquelle nous regardons un phénomène peut non seulement impacter les résultats d’une analyse mais peut conduire à des conclusions complètement contradictoires selon que nous optons pour une maille d’analyse ou une autre. Ce phénomène a été formulé par le statisticien Edward Simpson en 1951 et porte donc le nom du « paradoxe de Simpson ».
Parmi les exemples connus de ce paradoxe, une étude sur le tabagisme et les maladies cardiovasculaires a été menée en Grande Bretagne sur 1314 femmes pendant une vingtaine d’année. Les résultats de cette étude sont contre-intuitifs et étonnants : le taux de mortalité chez les fumeuses était de 23.9% contre 31.4% chez les non-fumeuses. Nous aurait-on menti ? Cette étude a-t-elle été financée par une grande compagnie de tabac ? Non, il s’agit simplement d’un exemple du paradoxe de Simpson.
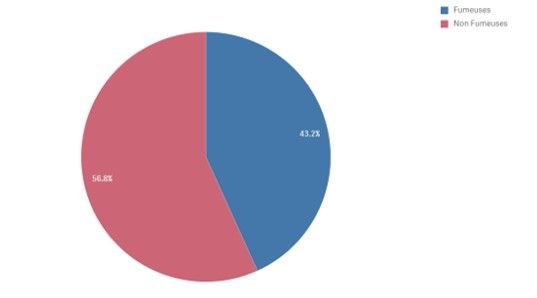
Taux de mortalité chez les femmes fumeuses et non fumeuses
Jusque-là, nous avons regardé les résultats de manière agrégée, à la maille la plus grande. Si nous analysons les mêmes chiffres à une maille plus fine, en analysant le taux de mortalité dans chaque tranche d’âge, les résultats sont les suivants.
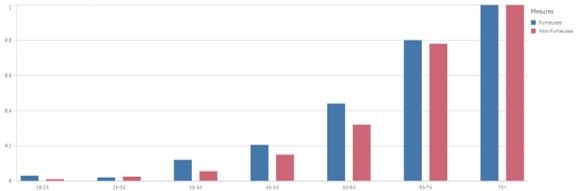
Taux de mortalité par tranche d’âge chez les fumeuses et non fumeuses
Les résultats du graphe ci-dessus sont plus intuitifs : Le taux de mortalité chez les fumeuses est plus grand dans quasiment toutes les tranches d’âge. Alors pourquoi les résultats changent en modifiant le groupe d’analyse ?
Rien de magique ! Il suffit de regarder la distribution de l’âge des femmes dans chaque catégorie pour comprendre que dans l’échantillon étudié, il y avait plus de femmes non fumeuses âgées de plus de 65 ans. C’est donc normal d’observer un taux de mortalité plus élevé chez cette catégorie, sauf que cela n’est très probablement pas dû à leur décision de ne pas fumer.
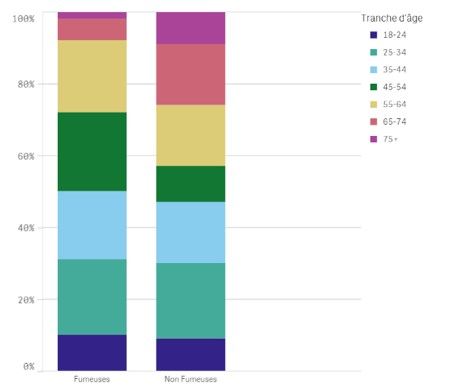
Répartition des fumeuses et non fumeuses par tranche d’âge
Le choix de la maille à laquelle nous analysons un problème constitue l’une des premières étapes qui se posent dans un projet de Machine Learning. C’est pourquoi il est toujours essentiel de vérifier l’existence de facteurs de confusion comme l’âge dans l’exemple de l’étude.
Si les statistiques sont indéniablement un outil essentiel en Data Science, il est toutefois nécessaire d’être avisé quant à leur utilisation et interprétation. Parfois, en essayant de faire parler les données, nous pouvons les forcer à dire ce que nous voulons.
Sources :
