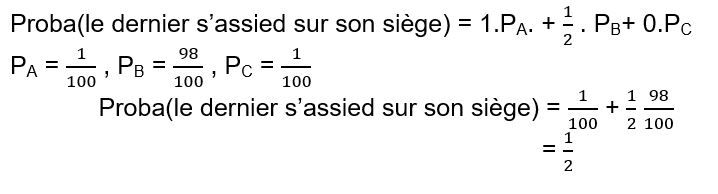Énigme
Dans un avion de 100 places plein, sans no-show ni overbooking, les passagers ont une place assignée, mais le premier passager à monter dans l’avion décide de s’installer où bon lui semble, au hasard.
Les autres passagers souhaitent s’assoir à leur place numérotée, mais si celle-ci est déjà prise, ils s’assoient au hasard à autre place.
Quelle est la probabilité que le dernier passager s’assoie à la place qui figure sur son billet ?
Solution
Lorsque les 99 premiers passagers se sont assis, selon les règles de l’énoncé, il reste soit le siège attribué au premier passager, soit celui attribué au 100e.
En effet, une fois chaque passager assis (sauf le premier), son siège est occupé. Soit il l’était déjà, soit il s’y est assis.
À chaque instant, si les sièges 1 et 100 sont disponibles, alors un passager choisissant au hasard a autant de chance de s’asseoir sur le siège 1 ou sur le siège 100. Donc rien ne les différencie en termes de probabilités.
Au début, il y a 3 configurations différentes :
A) Le premier s’assied sur son siège.
Alors chacun s’assied sur son propre siège et il reste le siège 100.
B) Le premier s’assied sur un des sièges 2 à 99.
Alors il y a une chance sur deux qu’il reste le siège 100 car les sièges 1 et 100 sont équiprobables.
C) Le premier s’assied sur le siège 100.
Alors chacun s’assied sur son propre siège et il reste le siège 1 à la fin.
CALCUL
Soit PA, PB et PC les probabilités que l’on soit respectivement dans les configurations A (le premier s’assied sur son siège), B et C.
La probabilité que le dernier s’asseye sur son siège est alors égale à :