Enigme
Pauline et Damien ont deux enfants, Samuel (2 ans) et Calixte (1 an). Les parents ont observé qu’ils passent une nuit correcte sur 3. C’est à dire que 2 nuits sur 3, l’un des enfants au moins se réveille.
Sachant que, pour un enfant, la probabilité de se réveiller la nuit est divisée par 2 tous les ans, dans combien de temps le nombre de nuits perturbées sera tombé à la fréquence acceptable d’une par semaine ?
Solution
A = Samuel se réveille,![]()
B = Calixte se réveille,![]()
Aujourd’hui, la probabilité que Pauline passe une nuit correcte est :![]()
En faisant l’hypothèse que![]() On a :
On a :
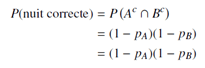
Samuel ayant 1 an de plus que Calixte, il se réveille 2 fois moins :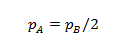
Aujourd’hui :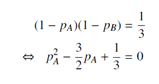
Les racines de ce polynôme sont 0.27 et 1.23. Les probabilités sont nécessairement inférieures à 1, donc la solution est 0.27.
On en déduit qu’aujourd’hui,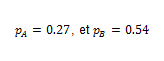
Dans n années,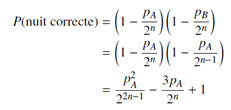
Donc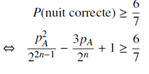
Pour trouver la solution à cette équation, on peut tester avec de nombreuses valeurs différentes de n, cela donne un graphique comme celui-ci :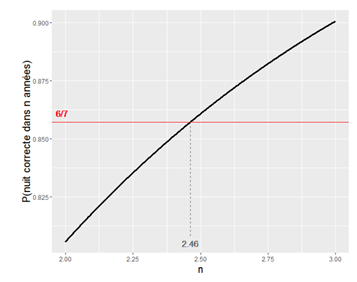
On trouve que la solution est 2.46.
Le nombre de nuits perturbées de Pauline et Damien sera tombé à la fréquence acceptable d’une par semaine (soit une nuit correcte supérieure à 6 sur 7) dans 2.46 ans.
