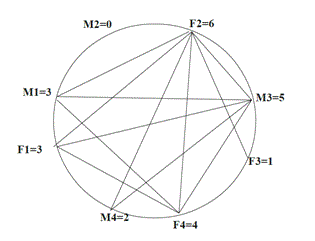
Enigme
M.et Mme Jacquet-Lagrèze assistent à une réunion. Il y a 3 autres couples dans l’assistance et plusieurs poignées de mains sont échangées.
On suppose que :
– Personne ne serre sa propre main
– Les époux ne se serrent pas la main entre eux
– Deux personnes quelconques de l’assemblée se serrent la main au plus une fois.
Monsieur Jacquet-Lagrèze constate que les 7 autres personnes ont échangé des poignées de mains en nombres tous distincts. Combien de poignées de mains M et Mme Jacquet-Lagrèze ont-ils échangées avec les autres membres de la réunion ?
Solution : C’est un problème de graphe !
Méthode de résolution n°1 :
Il faut construire un graphe, ou plutôt sa matrice d’incidence (il faut voir ça comme un sudoku !)
On numérote les personnes de 1 à 8, les couples sont les numéros successifs (ex : (1,2) forme un couple).
Il y 8 personnes au total, et elles ne serrent ni leur propre main ni celle de leur conjoint. Le nombre maximal de poignées de mains serrées par personne est donc 6. Les 7 personnes autres que M. Jacquet-Lagrèze ont donc respectivement serré 0, 1, 2, 3, 4, 5, 6 mains.
Voici la matrice de départ :
Les éléments diagonaux sont nuls car les gens ne peuvent pas serrer leur propre main. Ils ne peuvent pas non plus serrer celle de leur conjoint.
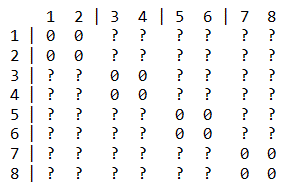
On place ensuite le chiffre 1 dans la case (i,j) si i sert la main à j ou vice versa. Dans le cas contraire, on met 0.
Puis, on résout un sudoku où la somme de chaque colonne / ligne doit être différente, à l’exception d’une colonne / ligne au maximum (ce sera celle de M. Jacquet-Lagrèze qui a constaté que « les 7 autres personnes ont échangé des poignées de mains en nombres tous distincts »).
Le résultat est donc le suivant :
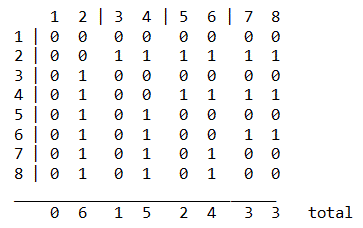
M. Jacquet-Lagrèze et son épouse ont serré 3 mains chacun !
Méthode de résolution n°2 (fournie par l’un de nos lecteurs !)
Mi et Fi désigne un couple. Il y a symétrie évidente entre homme et femme (interchangeables au sein d’un couple).
Si tous ont une valeur différente, à l’exception de M1 (à savoir M. Jacquet-Lagrèze qui a constaté que « les 7 autres personnes ont échangé des poignées de mains en nombres tous distincts »), toutes les valeurs de 0 à 6 sont prises une fois parmi les 7 invités.
Si l’un d’eux a 0, il s’exclue des possibilités pour tous ceux pouvant lui serrer la main, donc seul son conjoint peut avoir la valeur 6.
De proche en proche selon le même raisonnement, il y a complémentarité à 6 entre conjoints.
Et seul un couple peut être à égalité 3-3… M. Jacquet-Lagrèze et son épouse ont donc serré 3 mains chacun !