Enigme
La terrible algue Caulerpa taxifolia double de surface les jours pairs et triple de surface les jours impairs (en cours de journée). Au bout de 30 jours, elle a recouvert la totalité de la mer dans laquelle elle a par malheur été rejetée.
Au bout de combien de jours recouvrait-elle la moitié de la surface de cette mer ?
Solution
Résolution intuitive :
Puisque, au minimum, l’algue double de surface en un jour, elle doit avoir recouvert la moitié de la mer un jour avant d’en recouvrir la totalité. Il faut donc 29 jours pour que l’algue recouvre la moitié de la mer.
Résolution mathématique :
Notons s0 la surface initiale de l’algue (s0 ≠ 0), sM la surface totale de la mer.
Dire à la fois que l’algue double de surface les jours pairs et triple de surface les jours impairs revient à dire que la surface de l’algue se multiplie par 6 tous les deux jours. Ce qui peut être représenté comme dans le tableau suivant :
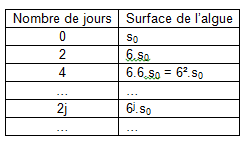
Ce tableau fournit l’expression de la surface de l’algue en fonction du nombre de jours de sa croissance et de sa surface initiale ; On peut modéliser l’évolution de cette algue par la fonction définie de N vers R par :
f(j) = 6(j/2).s0
Dire que l’algue a recouvert la totalité de la mer au bout de 30 jours se traduit par :
f(30) = sM.
Par suite,
sM = 615.s0
En désignant par k le nombre de jours au bout desquels l’algue recouvrirait la moitié de la surface de la mer, on a
f(k) = ½.sM
6(k/2).s0 = ½.615.s0,
6(k/2 -15) = ½
(k/2 – 15)ln6 = -ln2
Soit
k = 2(15 – 1/ln3) = 28,17952 = 29 jours.
