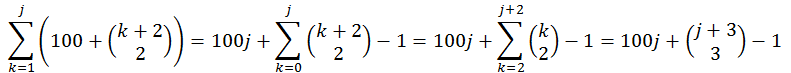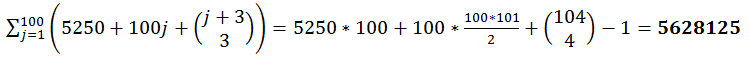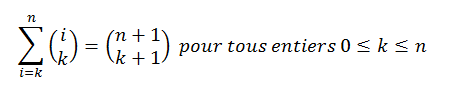Enigme
Alors qu’on croyait ces oiseaux disparus, M. Jean Payet a découvert des Dodos dans la Plaine des Tamarins. Il décide d’en faire commerce pour reverser les fonds gagnés à un organisme de protection de l’environnement de l’Océan Indien.
Une femelle Dodo pond un œuf chaque jour. Soit il vend cet œuf, soit il attend 100 jours pour avoir une autre Dodo pondeuse prête à pondre. Un œuf pondu le jour n donne alors une Dodo pondeuse le jour n+100, qui commence immédiatement à pondre.
M. Payet possède une Dodo femelle (et un Dodo mâle), qui commence à pondre le jour n°1.
Combien pourra-t-il avoir vendu d’œufs, au maximum, au bout de 400 jours ?
On suppose qu’il a toujours la chance d’obtenir des Dodos femelles.
Solution
Détermination de la stratégie optimale :
Il paraît logique de faire éclore les œufs au début pour avoir un maximum de Dodos puis les vendre à partir d’un certain jour n0. Comment déterminer ce jour ?
Prenons le cas d’un œuf pondu le jour n. Doit-on le faire éclore ou le vendre ?
- Si n>400-300=100, il ne sert à rien de le faire éclore puisque la Dodo qui en découlera ne pourra vendre des œufs avant la fin des 400 jours.
- Si n=300, c’est indifférent puisque dans tous les cas, on ne vendra qu’un œuf, le jour n°300 ou 400.
- Si n<300, il vaut mieux faire éclore l’œuf. Pour s’en convaincre, prendre un œuf pondu le jour n°299. Si on le vend, cela nous fait un œuf alors que si on le fait éclore, la Dodo résultante pondra des œufs les jours 299+100=399 et 400.
La stratégie optimale est donc de faire systématiquement éclore les œufs jusqu’au jour n0=299 ou 300 puis de les vendre. On choisit n0=300.
Dénombrement des Dodos et des œufs :
On va raisonner par période de 100 jours afin de délimiter les générations de Dodos.
Ainsi, pour j=1 à 100 :
- La première Dodo pond un œuf le jour j (c’est la seule Dodo).
- Le jour j+100, la Dodo issue de l’œuf pondu le jour j se met à pondre. Ce jour j+100, le nombre d’œufs pondus est donc de 1+j (par la Dodo de première génération et les j Dodos de seconde génération). Au jour 200, on a donc 1+100=101 Dodos pondeuses.
- Le jour j+200, les j+1 Dodos issues des œufs pondus le jour j+100 se mettent à pondre. Combien a-t-on de telles Dodos de 3e génération le jour j+200 ? Elles sont:
Au jour j+200, le nombre d’œufs pondus est donc de 
Il y a donc notamment 5251 Dodos pondeuses le jour 300.
- Le jour j+300, les
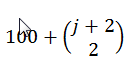Dodos issues des œufs pondus le jour j+200 commencent à pondre. Le nombre d’œufs pondus par ces Dodos de 3ème génération est donc de:
Le nombre d’œufs pondus le jour j+300 est donc de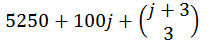 
Il n’y a ensuite plus qu’à sommer le nombre d’œufs vendus entre le jour 301 et le jour 400 :
PS : On a utilisé à deux reprises la proposition suivante qui se démontre par sommation télescopique de la formule de Pascal :
