Enigme
A l’origine le rugby suivait des règles différentes que celles actuelles : la marque y était différente, et on ne transformait pas les essais.
Bien sûr, comme actuellement, une pénalité rapportait moins qu’un essai, mais il y avait tout de même 91 scores impossibles à obtenir ; l’un de ces scores était 48.
Combien de points rapportait une pénalité ? Combien de points rapportait un essai ?
Solution
Soit P la valeur d’une pénalité.
Soit E la valeur d’un essai.
Soit N le nombre de scores inatteignables.
Soit N1 le nombre de scores inatteignables sur l’intervalle [0,E*P]
Soit N2 le nombre de scores inatteignables sur l’intervalle ]E*P,+INF[
———————————————————————–
Les hypothèses sont :
– P et E entiers positifs (avec P<E);
– N = 91;
– P et E ne sont pas des diviseurs de 48 (Il n’existe pas de u et v entiers tel que P*u+E*v= 48).
On en déduit que :
– P et E premiers entre eux (sinon N serait infini).
Les propriétés suivantes sont donc vérifiées :
– Il existe u et v deux entiers relatifs tel que P*u + E*v = 1 (définition de nombre premier entre eux).
– PPCM(E,P) = E*P (car PGCD(E,P) = 1 et PGCD(E,P)*PPCM(E,P)=E*P)
Remarquons que le score E*P est un score atteignable.
Dans la relation P*u+E*v=1, soit u >= 0, soit v >=0. On suppose que u >= 0 (le cas v>=0 aboutit à la même chose) On a donc :
E*P+1 = E*P + P*u +E*v
= E*(P+v)+P*u
Montrons qu’il existe un v tel que P+v est positif.
Supposons que P+v <= 0 c’est-à-dire P <= -v on a alors :
E*P <= -E*v (car E > 0)
E*P – P*u <= -E*v –P*u
P*(E-u) <= -1 < 0
Or P > 0 Donc E < u
On peut donc écrire u=E+u1 et -v=P+v1 avec |v1| < |v| et u1 entier positif.
Or 1 = P*u+E*v
1 = P*(E+u1)+E*(-P-v1)
1 = P*E+P*u1-P*E-E*v1
1 = P*u1+E*(-v1)
On a donc trouvé deux entiers relatifs qui respectent la propriété, tel que : u1 > 0
Et |v1| < v. Il est donc possible de répéter la procédure de manière à trouver un v1 tel que |v1| < P et u1 > 0.
On a donc :
E*P+1 = E*P + P*u +E*v
= E*(P+v)+P*u est également un score atteignable avec u > 0 et P+v > 0
Tout comme : (E*P+2)=(E*P+1)+1, ….
On en déduit que sur l’intervalle ]E*P, +INF[ tous les scores sont atteignables donc N2 = 0 et N = N1
———————————————————————–
Nous allons maintenant comptabiliser le nombre Q de scores atteignables dans l’intervalle [0, E*P].
Un score X atteignable sur cet intervalle doit respecter les conditions suivantes :
– X = a*P + b*E avec a et b deux entiers positifs
– a Æ [0,E], soit E+1 valeurs
– b Æ [0,P], soit P+1 valeurs
– X <= P*E
On remarque que :
– X=P*E peut s’obtenir en utilisant le couple (a,b) = (0,P) ou (E,0).
Montrons qu’il n’y a que ces deux possibilités pour obtenir cette valeur.
Soit un couple (a’, b’) vérifiant a’*P+E*b’=P*E
On a donc: P*(E-a) = E*b = K1 et P*a = E*(P-b)=K2
On remarque donc que K1 et K2 sont des multiples communs de P et de E. Or PPCM(E,P)=E*P. On a donc K1 >= E*P et K2 >= E*P.
On obtient alors les systèmes d’inéquations suivantes :
Pour K1 : P*(E-a) >= P*E et E*b>= E*P implique a=0 et b=P
Pour K2 : P*a >= P*E et E*(P-b) >= E*P implique a=E et b=0
Les seuls couples possibles sont donc (0,P) et (E,0).
———————————————————————–
– Pour tout X < P*E, il n’existe qu’un seul couple (a,b) pour obtenir la valeur X.
En effet, supposons qu’il existe un autre couple (a’,b’) différent de (a,b) tel que X=a*P+b*E=a’*P+b’*E (Dans ce cas on suppose a’ > a et b’ < b (le cas a’ < a et b’ > b aboutit à la même chose).
On a donc (a’-a)*P = (b-b’)*E = K
Or 0 < a’ – a < E et 0 < b- b’ < P
On a donc: 0 < (a’ – a)*P < E*P et 0 < (b- b’)*E < P*E
Il existe donc K, tel que 0 < K < P*E et K multiple de P et de E.
Or PPCM(E,P) = E*P et K < P*E, multiple de P et E -> Il y a un problème donc l’hypothèse est fausse. Il n’existe donc pas d’autre couple définissant X sur l’intervalle [0, E*P[.
———————————————————————–
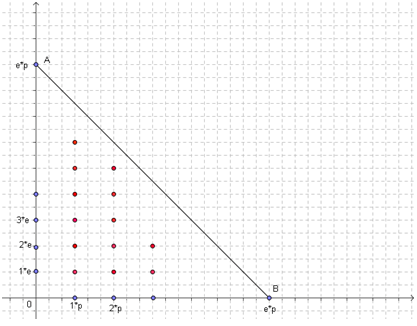
On peut alors représenter l’ensemble des scores atteignables de la façon suivante : l’axe des ordonnées représente les valeurs de a possibles et l’axe des abscisses représente les valeurs de b possibles. La droite reliant les points b=(0,E*P) et a=(E*P,0) représente la contrainte X <= P*E. L’ensemble des points colorés du graphe ci dessous représente l’ensemble des scores atteignables.
Il s’agit donc de la moitié des points du rectangle de côté e+1 et p+1, on a donc : Q = ([(E+1)*(P+1)]/2)-1
Le –1 est là car X=P*E peut s’obtenir de deux façons (seul point dans ce cas) !
Dans l’intervalle [0, E*P] on a donc : N1 = N
N = E*P-[([(E+1)*(P+1)]/2)-1]
N = [2*E*P-((E*P+E+P+1)-2)]/2
2N = [2*E*P-(E*P)-E-P+1]
2N = [E*P-E-P+1]
2N = (E-1)*(P-1)
182 = (E-1)*(P-1) (Rappel : ici N=91)
Ensuite on énumère, les possibilités pour P et E :
– Si P = 2 alors E = 183 mais 48 est atteignable (48 = 2 * 24)
– Si P = 3 alors E = 92 mais 48 est atteignable (48 = 3 * 16)
– Si P = 4,5… E n’est pas dans Z
– Si P = 8 alors E = 27 mais 48 est atteignable (48 = 8 * 6)
– Si P = 14 alors E = 15 et 48 n’est pas atteignable
En conclusion, à l’origine du rugby, une pénalité rapportait 14 points , et un essai rapportait 15 points.