Problème
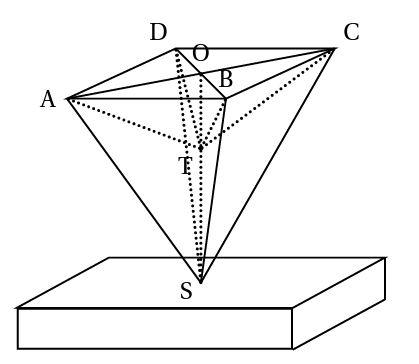
Cette figure représente une fontaine en pierre ; il s’agit d’une pyramide régulière SABCD dans laquelle on a creusé une pyramide régulière TABCD correspondant au bassin qui reçoit l’eau. SABCD a pour base le carré ABCD de centre O, de côté AB = 6, et pour hauteur SO = 9.
(Les longueurs sont données en dm.)
Première partie :
Dans cette partie, OT = 6.
1) a) Calculer le volume du bassin TABCD.
b) Donner sa capacité en litres.
2) Démontrer que le volume de pierre de la fontaine est de 36 dm3.
Deuxième partie :
On s’intéresse ici au cas où les faces latérales de TABCD sont des triangles équilatéraux.
1) Donner la valeur de AT.
2) Dans le triangle ABC, calculer AC. On donnera la réponse sous la forme a![]() , avec a et b entiers et b le plus petit possible.
, avec a et b entiers et b le plus petit possible.
3) En utilisant la réciproque du théorème de Pythagore, démontrer que le triangle ACT est rectangle.
Troisième partie :
Dans cette partie, OT = x.
1) Quelles sont les valeurs de x possibles ?
2) Exprimer le volume de pierre de la fontaine en fonction de x.
3) Représenter la fonction f : x ![]() 108 – 12x .
108 – 12x .
4) Retrouver, à l’aide de tracés en pointillés sur le graphique, le résultat de la partie A 2°).
5) a) Par lecture graphique, donner une valeur approchée de x pour que le volume de pierre de la fontaine soit 80 dm3.
b) Trouver la valeur exacte de x en résolvant l’équation 108 – 12x = 80.
